Excelの行列検索の最終形としてINDEXと2つのMATCH(またはXMATCH)を組み合わせる方法を学びました。しかし、Microsoft 365の登場で、このテクニックはさらなる進化を遂げました。
それが「動的配列(スピル)」機能です。これにより、従来であれば一つずつ数式をコピー&ペーストしていた作業が、たった一つの数式を入力するだけで、関連するセルすべてに結果を自動で表示できるようになりました。今回は、この革新的な機能を使った一括データ抽出の方法を解説します。
今回のゴール:複数の氏名・複数の項目を「単一の数式」で一気に取り出す
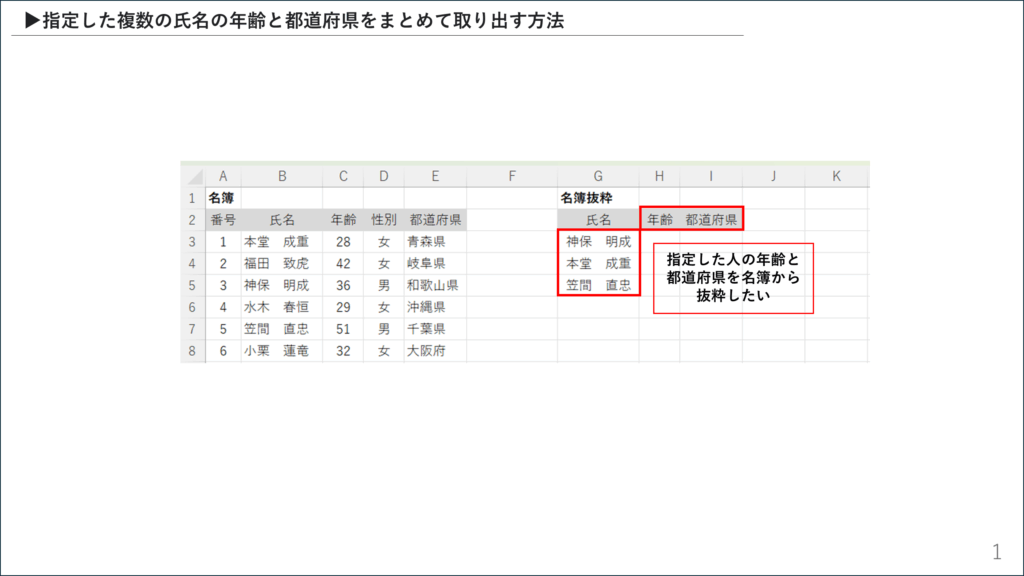
左側の「名簿」から、右側の「名簿抜粋」にリストアップされた3人分の「年齢」と「都道府県」を抽出します。この時、
H3セルに一度だけ数式を入力するだけで、H3からI5までの6つのセルすべてに結果を表示させることが目標です。 1111
サンプルデータ
以下は、上記画像のExcelデータですので、ダウンロードして練習として使用ください。
Excel-g731-1.xlsx (ダウンロード)
この機能を試すために、以下のサンプルデータをExcelシートにコピーしてください。
| A | B | C | D | E | F | G | H | I | |
| 1 | 名簿 | 名簿抜粋 | |||||||
| 2 | 番号 | 氏名 | 年齢 | 性別 | 都道府県 | 氏名 | 年齢 | 都道府県 | |
| 3 | 1 | 本堂 成重 | 28 | 女 | 青森県 | 神保 明成 | (数式はここに) | ||
| 4 | 2 | 福田 致広 | 42 | 女 | 岐阜県 | 本堂 成重 | |||
| 5 | 3 | 神保 明成 | 36 | 男 | 和歌山県 | 笠間 直忠 | |||
| 6 | 4 | 水木 春恒 | 29 | 女 | 沖縄県 | ||||
| 7 | 5 | 笠間 直忠 | 51 | 男 | 千葉県 | ||||
| 8 | 6 | 小栗 蓮竜 | 32 | 女 | 大阪府 |
解決策:動的配列に対応した INDEX & XMATCH
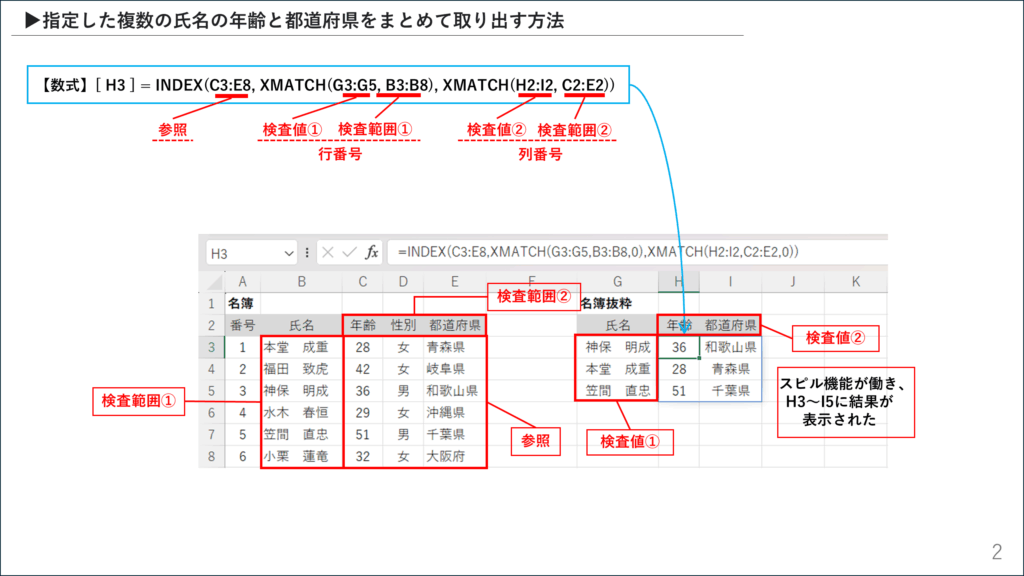
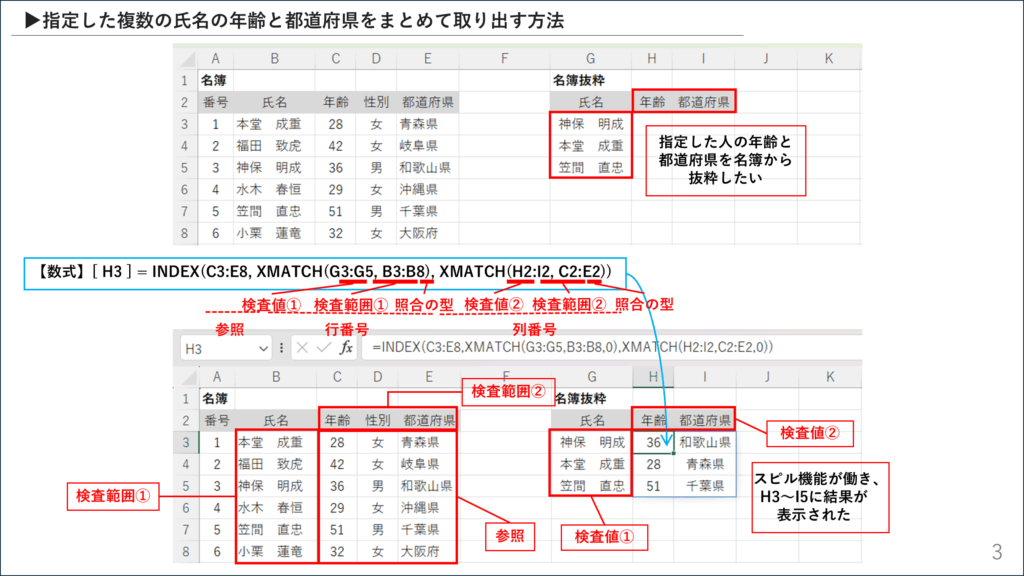
セルH3に、以下の数式を一度だけ入力します。
Excel
=INDEX(C3:E8, XMATCH(G3:G5, B3:B8), XMATCH(H2:I2, C2:E2))
数式を入力してEnterキーを押すと、魔法のように
H3:I5の範囲全体に結果が自動で展開(スピル)されます。 2222
数式の解説(なぜ1つの数式で全てが埋まるのか?)
この数式が動的配列として機能する秘訣は、XMATCH関数の引数に単一のセルではなく、セル範囲を渡している点にあります。
1. XMATCHで行番号の「配列」を取得する
XMATCH(G3:G5, B3:B8)
- 従来は
G3のように単一のセルを検索値としていましたが、ここではG3:G5という範囲を指定しています。 - これにより、
XMATCHはG3,G4,G5の各氏名が、名簿B3:B8の何番目にあるかを一度に計算し、結果を**配列(値のリスト)**として返します。- 例:「神保 明成」→3番目、「本堂 成重」→1番目、「笠間 直忠」→5番目
- 結果として
{3; 1; 5}のような縦の配列が生成されます。
2. XMATCHで列番号の「配列」を取得する
XMATCH(H2:I2, C2:E2)
- 同様に、列の検索値も
H2:I2という範囲で指定します。 - これにより、
XMATCHは「年齢」と「都道府県」が、見出しC2:E2の何番目にあるかを一度に計算します。- 例:「年齢」→1番目、「都道府県」→3番目
- 結果として
{1, 3}のような横の配列が生成されます。
3. INDEXが配列を受け取り、結果をスピルさせる
最終的に、INDEX関数は以下のような命令を受け取ったことになります。
=INDEX(C3:E8, {3; 1; 5}, {1, 3})
INDEX関数は、行番号と列番号に配列が渡されると、それらの組み合わせからなる**行列(マトリクス)**の結果を返そうとします。- 「3行目の1列目と3列目」「1行目の1列目と3列目」「5行目の1列目と3列目」…という全ての組み合わせの結果を計算し、出力先のセルに自動で展開します。これが「スピル」です。
まとめ
Microsoft 365の動的配列機能は、Excelの数式の概念を大きく変えました。INDEXとXMATCH(またはMATCH)の組み合わせにこの機能を用いることで、複数の検索をたった一つの数式で、瞬時に、そしてエラーなく実行できます。
- 効率性: 数式をコピー&ペーストする必要が一切ない。
- 保守性: 修正は
H3セルの数式一つで済む。 - 可読性: 処理の内容が単一の数式に集約されているため、分かりやすい。
これからのExcelの標準となるこのパワフルな機能をぜひマスターして、日々のデータ集計作業を劇的に効率化してください。









コメント