はじめに
Excelには様々な統計関数が用意されていますが、PHI関数(およびNORM.S.DIST関数)は、標準正規分布における確率密度を計算する際に役立ちます。確率密度とは、ある特定のz値における「高さ」のようなもので、その値を取る確率そのものではありません。確率を求めるには、確率密度を積分する必要があります(つまり、グラフの下の面積を求めることになります)。この記事では、PHI関数と、より現代的なNORM.S.DIST関数の使い方を詳しく解説します。
標準正規分布とは?
標準正規分布は、正規分布の中でも特に重要な分布で、以下の特徴を持ちます。
- 平均 (μ): 0
- 標準偏差 (σ): 1
PHI関数とは?
PHI関数は、標準正規分布の確率密度関数(PDF)の値を返します。
基本的な構文
Excel
=PHI(x)
各引数の意味は以下の通りです。
- x(必須): 標準正規分布における値を指定します(z値)。
NORM.S.DIST関数とは?
NORM.S.DIST関数は、標準正規分布の確率密度関数(PDF)または累積分布関数(CDF)の値を返します。PHI関数の代わりにこちらを使用することが推奨されています。
基本的な構文
Excel
=NORM.S.DIST(x, cumulative)
各引数の意味は以下の通りです。
- x(必須): 標準正規分布における値を指定します(z値)。
- cumulative(必須): 論理値で、関数の種類を指定します。
- TRUE: 累積分布関数(CDF)を返します。
- FALSE: 確率密度関数(PDF)を返します。
画像例の解説
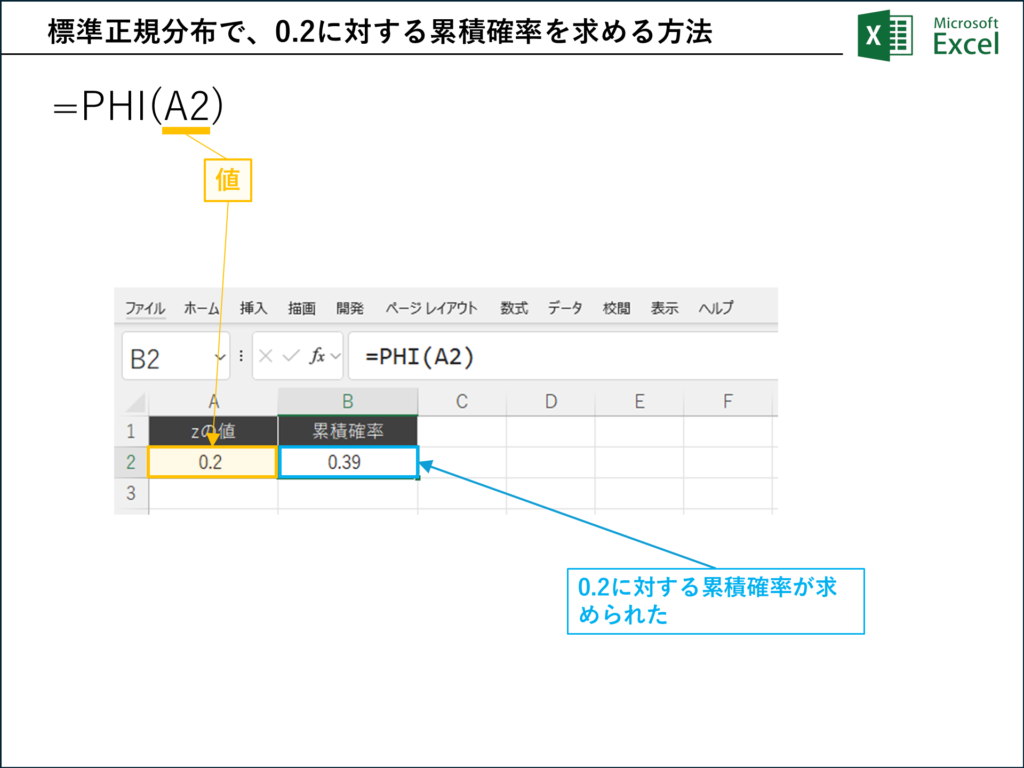
画像では、以下の設定でPHI関数を使用しています。
- z値: セルA2に0.2が入力されています。
- 数式: セルB2には以下の数式が入力されています。
Excel
=PHI(A2)
この数式を分解して解説します。
- A2: z値(0.2)を指定しています。
数式の動作
この数式は、「標準正規分布において、z値が0.2の確率密度」を計算します。結果として、セルB2には0.3989(約0.39)と表示されています。これは、z=0.2における標準正規分布のグラフの「高さ」を表しています。
Excelサンプルデータのダウンロード
上記画像のエクセルサンプルデータを、以下のリンクからダウンロードし、練習用として活用ください。
【Excel】練習用サンプルデータ(例題)をダウンロード(無料)
NORM.S.DISTを使った場合
同じ結果をNORM.S.DIST関数で得るには、以下の数式を使用します。
Excel
=NORM.S.DIST(A2, FALSE)
この数式も、z値0.2に対する確率密度を計算し、PHI関数と同じ結果を返します。
例:正規分布のグラフ
確率密度は、正規分布のグラフを描く際に使用されます。例えば、様々なz値に対する確率密度を計算し、それらをグラフにプロットすることで、標準正規分布の釣鐘型のグラフを作成することができます。
PHI関数の注意点
- 引数に数値以外の値を指定すると、エラー値 #VALUE! が返されます。
- PHI関数は標準正規分布(平均0、標準偏差1)にのみ適用されます。
NORM.S.DIST関数の注意点
- 引数に数値以外の値を指定すると、エラー値 #VALUE! が返されます。
まとめ
PHI関数は、標準正規分布の確率密度を計算する簡単な方法を提供しますが、現代のExcelではNORM.S.DIST関数を使用することが推奨されています。NORM.S.DIST関数は、確率密度だけでなく累積確率も計算できるため、より汎用性があります。これらの関数を理解することで、正規分布に関する様々な計算をExcelで行うことができるようになります。
この解説で、PHI関数とNORM.S.DIST関数について、より深く理解できたかと思います。この情報を活用し、Excelでのデータ分析をより効率的に行いましょう。










コメント