449-01｜線形回帰分析における回帰直線の標準誤差を計算する｜Excel STEYX関数

ExcelのSTEYX関数は、線形回帰分析における回帰直線の標準誤差を計算するための関数です。この標準誤差は、回帰モデルの予測精度や信頼性を評価する際に非常に重要です。本記事では、STEYX関数の使い方とその活用方法について詳しく解説します。

関数の説明

STEYX関数とは？

STEYX関数は、指定したxおよびyデータセットに基づいて回帰直線の標準誤差を計算します。標準誤差は、回帰直線からのデータポイントの分散を示し、回帰分析の結果がどれだけ信頼できるかを評価するために使用されます。標準誤差が小さいほど、回帰モデルの予測精度が高いことを示します。

関数

対応バージョン

• Excel 2007以降

構文

=STEYX(known_y's, known_x's)

引数

引数	説明
known_y’s	必須。回帰分析のための既知のy値（応答変数）のデータセットです。
known_x’s	必須。回帰分析のための既知のx値（説明変数）のデータセットです。

関数作成のポイント

• known_y's と known_x's は同じ数のデータポイントを持つ必要があります。
• データセットが適切に整列されていることを確認してください。

関数活用のポイント

• 回帰直線の精度を評価するために使用し、予測値の信頼性を向上させるために役立ちます。
• 統計的な分析やモデル評価において、データのばらつき具合を理解するために使用します。

使用例

サンプルデータ

A	B
月	売上
1月	100
2月	120
3月	130
4月	150
5月	160

サンプル式

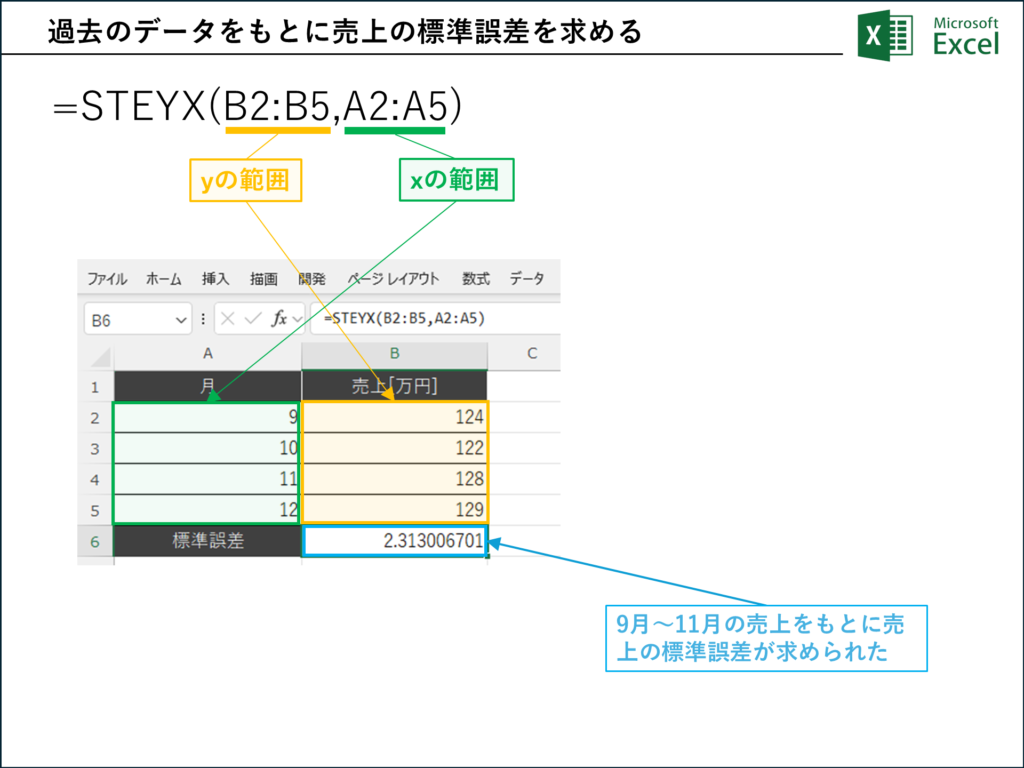
=STEYX(B2:B6, A2:A6)

この式は、月ごとの売上データを基に回帰直線の標準誤差を計算します。標準誤差が小さいほど、回帰直線がデータポイントに適合していることを示します。

（例題）サンプルデータダウンロード

サンプルデータをダウンロードすることができます。以下のリンクからダウンロードしてください。

【Excel】練習用サンプルデータ（例題）をダウンロード（無料）

まとめ

STEYX関数は、回帰直線の標準誤差を計算するための便利なツールです。回帰分析におけるモデルの信頼性や予測精度を評価するために、適切に活用してください。データ分析や統計的な評価において、精度の高い予測を実現するために役立ちます。

関連のある関数

関数	説明
LINEST	回帰直線の係数や統計データを計算する関数で、回帰直線の傾きや切片を求める際に使用します。
SLOPE	回帰直線の傾きを計算する関数で、データセットの勾配を求めます。
INTERCEPT	回帰直線のy切片を計算する関数で、xが0のときのyの値を求めます。

この記事では、STEYX関数の基本的な使い方とその応用方法について説明しました。回帰分析におけるモデルの精度を評価するために、積極的に活用してください。