はじめに
Excelには様々な数学関数が用意されていますが、GAMMALN.PRECISE関数とGAMMALN関数は、数値のガンマ関数の自然対数を計算する際に役立ちます。ガンマ関数は階乗の一般化であり、統計学、確率論、物理学など様々な分野で応用されています。特に、ガンマ関数の値が非常に大きくなる場合、その自然対数を扱うことで数値計算上の問題を回避できるため、GAMMALN関数とその高精度版であるGAMMALN.PRECISE関数は重要です。この記事では、GAMMALN.PRECISE関数とGAMMALN関数の基本的な使い方から、画像にある例、そしてExcelのバージョン情報までを詳しく解説します。
ガンマ関数と自然対数とは?
ガンマ関数(Γ(x)と表記)は、階乗の概念を複素数に拡張した関数です。正の整数 n に対しては、Γ(n) = (n-1)! が成り立ちます。
自然対数(ln(x)と表記)は、ネイピア数 e (約2.71828) を底とする対数です。つまり、e^y = x のとき、ln(x) = y となります。
GAMMALN関数とその高精度版であるGAMMALN.PRECISE関数は、ガンマ関数値Γ(x)の自然対数ln(Γ(x))を計算します。
GAMMALN.PRECISE関数とGAMMALN関数とは?
GAMMALN.PRECISE関数とGAMMALN関数は、Excelでガンマ関数の自然対数を計算するための関数です。
基本的な構文
Excel
=GAMMALN.PRECISE(数値)
Excel
=GAMMALN(数値)
各引数の意味は以下の通りです。
- 数値(必須): ガンマ関数の自然対数を計算する数値を指定します。正の数値を指定します。
Excelバージョン情報:GAMMALN.PRECISEとGAMMALN
GAMMALN関数は、Excel 2007で導入されました。GAMMALN.PRECISE関数は、Excel 2010で導入されました。GAMMALN.PRECISE関数は、特に数値が大きい場合に、より高い精度で計算を行います。通常はGAMMALN.PRECISEを使用することを推奨します。
画像例の解説
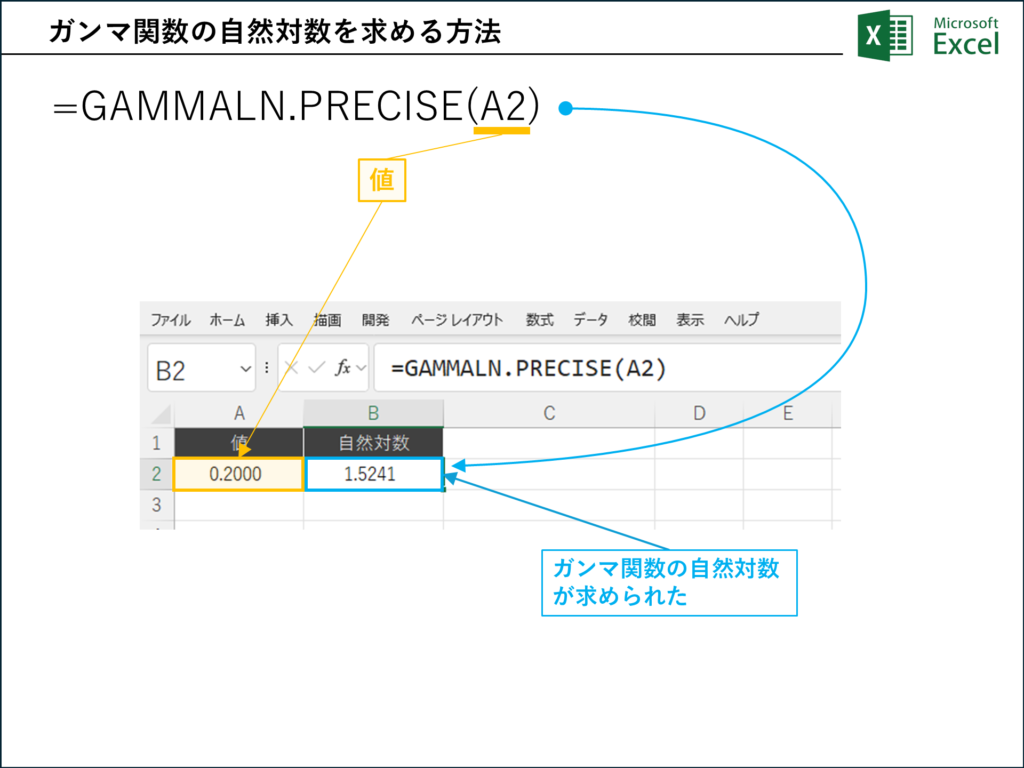
画像では、以下の設定でGAMMALN.PRECISE関数を使用しています。
- 数値: セルA2に0.2が入力されています。
- 数式: セルB2には以下の数式が入力されています。
Excel
=GAMMALN.PRECISE(A2)
この数式を分解して解説します。
- A2: 数値(0.2)を指定しています。
数式の動作
この数式は、数値0.2のガンマ関数の自然対数を計算します。結果として、セルB2には1.5241…(約1.5241)と表示されています。
Excelサンプルデータのダウンロード
上記画像のエクセルサンプルデータを、以下のリンクからダウンロードし、練習用として活用ください。
【Excel】練習用サンプルデータ(例題)をダウンロード(無料)
GAMMALN.PRECISE関数とGAMMALN関数の違い
GAMMALN.PRECISE関数は、GAMMALN関数よりも計算精度が高いです。特に、数値が大きい場合や、より正確な結果が必要な場合は、GAMMALN.PRECISE関数を使用することを推奨します。通常は、GAMMALN.PRECISE関数を使用すれば問題ありません。
GAMMALN.PRECISE/GAMMALN関数の応用例
GAMMALN.PRECISE/GAMMALN関数は、以下の場面で役立ちます。
- 統計学: ガンマ分布、ベータ分布など、様々な確率分布に関連する計算に用いられます。特に、確率密度関数や尤度関数の計算で、数値のオーバーフローやアンダーフローを防ぐために、対数変換が用いられる場合に役立ちます。
- 機械学習: 機械学習の分野でも、確率モデルの計算などで使用されます。
例:ガンマ分布の確率密度関数の計算(対数表現)
ガンマ分布の確率密度関数を直接計算すると、数値が非常に小さくなったり大きくなったりして計算が不安定になることがあります。そこで、対数変換を行い、計算を安定させることがあります。
例えば、α=2、β=3、x=4の場合の確率密度関数の自然対数を計算するには、Excelで以下のように計算できます。
Excel
=LN(4*(EXP(-4/3))/(9*EXP(GAMMALN.PRECISE(2))))
または、変形して以下のように計算することもできます。
Excel
=LN(4)-4/3-LN(9)-GAMMALN.PRECISE(2)
このように、GAMMALN.PRECISE関数を使用することで、計算が簡単になり、数値の安定性も向上します。
GAMMALN.PRECISE/GAMMALN関数の注意点
- 数値が0以下の場合、エラー値 #NUM! が返されます。
- 引数に数値以外の値を指定すると、エラー値 #VALUE! が返されます。
まとめ
GAMMALN.PRECISE関数とGAMMALN関数は、数値のガンマ関数の自然対数を簡単に計算できる非常に便利な関数です。統計学や確率論などで頻繁に使用されます。Excel 2010以降を使用している場合は、高精度なGAMMALN.PRECISE関数を活用することで、より正確な計算を行うことができます。
この解説で、GAMMALN.PRECISE関数とGAMMALN関数について、より深く理解できたかと思います。この情報を活用し、Excelでのデータ分析をより効率的に行いましょう。
この解説に加えて、以下のような内容を含めると、さらに充実した記事になります。
- ガンマ関数のグラフと自然対数の関係: グラフを掲載することで、関数の挙動を視覚的に理解しやすくなります。
- 他の関連数学関数との比較: GAMMA関数など、他の関連関数との違いを明確にすることで、GAMMALN.PRECISE/GAMMALN関数の特性をより深く理解できます。
- 具体的な応用例の詳細: ガンマ分布を用いた具体的な問題例とその解法を示すことで、読者の理解が深まります。
- エラー処理の詳細: 引数に不正な値を入力した場合にどのようなエラーが発生するか、またその対処法などを具体的に記述することで、より実用的な記事になります。










コメント