503｜Excel GAMMA.INV関数とGAMMAINV関数：ガンマ分布の逆関数を計算

はじめに

Excelには様々な統計関数が用意されていますが、GAMMA.INV関数は、ガンマ分布の累積確率から対応する値を求める際に役立ちます。これは、ある確率に対応するガンマ分布上の値を知りたい場合に有用です。この記事では、GAMMA.INV関数の基本的な使い方から、画像にある例、そしてExcelのバージョン情報、さらに旧バージョンのGAMMAINV関数についても詳しく解説します。

ガンマ分布と逆関数とは？

ガンマ分布は、正の実数値をとり、形状パラメータαと尺度パラメータβによって特徴付けられる連続確率分布です。累積分布関数（CDF）は、ある値x以下の確率を表します。逆関数（逆累積分布関数またはパーセント点関数とも呼ばれる）は、与えられた確率に対応するxの値を返します。つまり、GAMMA.DIST(x, α, β, TRUE) = p のとき、GAMMA.INV(p, α, β) = x となります。

GAMMA.INV関数とは？

GAMMA.INV関数は、Excelでガンマ分布の逆関数を計算するための関数です。

基本的な構文

Excel

=GAMMA.INV(確率, α, β)

各引数の意味は以下の通りです。

• 確率（必須）: ガンマ分布の累積確率を指定します。0より大きく1より小さい数値を指定します。
• α（必須）: 形状パラメータを指定します。正の数値を指定します。
• β（必須）: 尺度パラメータを指定します。正の数値を指定します。

Excelバージョン情報：GAMMA.INVとGAMMAINV

GAMMA.INV関数は、Excel 2010で導入されました。それ以前のバージョンでは、GAMMAINV関数を使用していました。GAMMAINV関数はGAMMA.INV関数とほぼ同じ機能を持っていますが、GAMMA.INV関数の方がより現代的な命名規則に従っています。GAMMAINV関数は互換性のために残されていますが、新しいバージョンではGAMMA.INVを使用することを推奨します。

画像例の解説

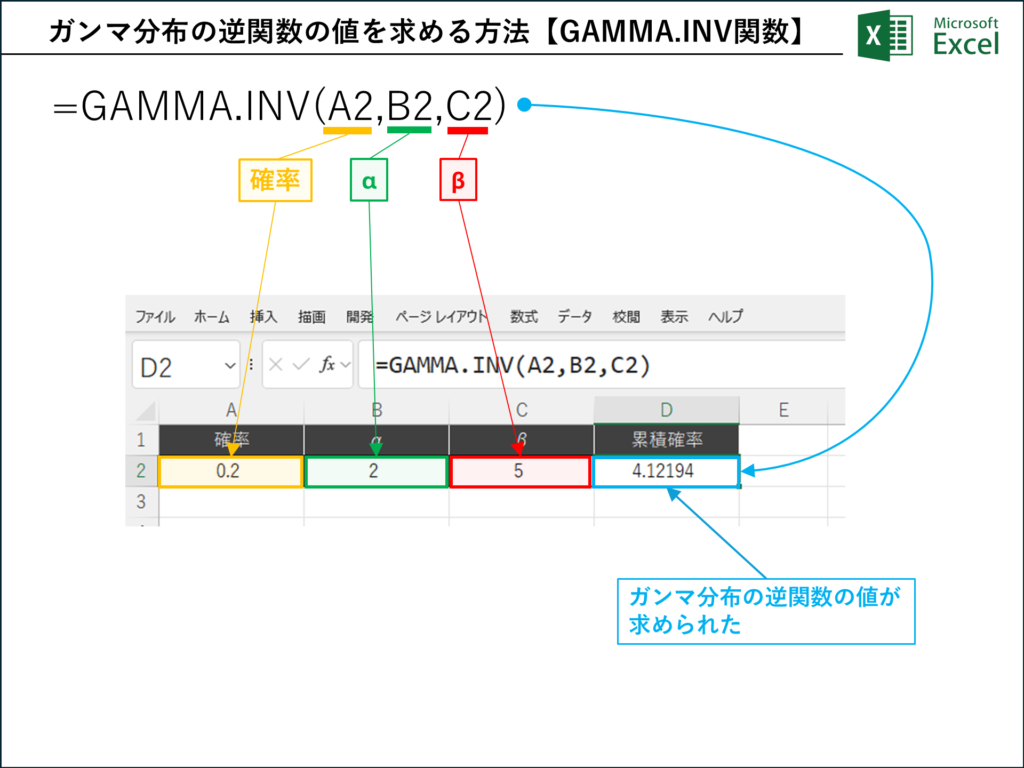
画像では、以下の設定でGAMMA.INV関数を使用しています。

• 確率: セルA2に0.2が入力されています。
• α（形状パラメータ）: セルB2に2が入力されています。
• β（尺度パラメータ）: セルC2に5が入力されています。
• 数式: セルD2には以下の数式が入力されています。

Excel

=GAMMA.INV(A2,B2,C2)

この数式を分解して解説します。

1. A2: 確率として0.2を指定しています。
2. B2: 形状パラメータαとして2を指定しています。
3. C2: 尺度パラメータβとして5を指定しています。

数式の動作

この数式は、「形状パラメータが2、尺度パラメータが5のガンマ分布において、累積確率が0.2となるxの値」を計算します。結果として、セルD2には4.12194…（約4.12194）と表示されています。

Excelサンプルデータのダウンロード

上記画像のエクセルサンプルデータを、以下のリンクからダウンロードし、練習用として活用ください。

【Excel】練習用サンプルデータ（例題）をダウンロード（無料）

GAMMAINV関数（古いバージョン）

Excelの古いバージョン（Excel 2007以前など）では、GAMMAINV関数を使用していました。GAMMAINV関数の構文は以下の通りです。

Excel

=GAMMAINV(確率, α, β)

引数の意味はGAMMA.INV関数と同じです。

例：信頼区間の計算

ある試験の結果がガンマ分布に従うとします。形状パラメータαが3、尺度パラメータβが10である場合、上位95%の信頼区間の下限値を求めます。これは、累積確率が0.05となる値を求めることに相当します。

ExcelでGAMMA.INV関数を使用すると、

Excel

=GAMMA.INV(0.05,3,10)

と入力します。

GAMMA.INV関数の注意点

• 確率が0以下または1以上の場合は、エラー値 #NUM! が返されます。
• αまたはβが0以下の場合も、エラー値 #NUM! が返されます。
• 引数に数値以外を指定すると、エラー値 #VALUE! が返されます。

まとめ

GAMMA.INV関数は、ガンマ分布の累積確率から対応する値を求める際に非常に役立つ関数です。信頼区間の計算や、特定の確率に対応する値を知りたい場合などに使用されます。最新のExcelを使用している場合は、GAMMA.INV関数を使用し、古いバージョンを使用している場合はGAMMAINV関数を使用することを覚えておきましょう。

この解説で、GAMMA.INV関数とGAMMAINV関数について、より深く理解できたかと思います。この情報を活用し、Excelでのデータ分析をより効率的に行いましょう。

---

この解説に加えて、以下のような内容を含めると、さらに充実した記事になります。

• ガンマ分布のグラフと逆関数の関係: グラフを掲載することで、累積確率と逆関数の関係を視覚的に理解しやすくなります。
• 具体的な応用例の詳細: 信頼区間の計算以外にも、在庫管理、保険数理など、具体的な応用例を示すことで、読者の理解が深まります。
• GAMMA.DIST関数との関係: GAMMA.DIST関数と組み合わせて使用する例を示すことで、両関数の関係が明確になります。
• エラー処理の詳細: 引数に不正な値を入力した場合にどのようなエラーが発生するか、またその対処法などを具体的に記述することで、より実用的な記事になります。