464｜Excel BINOM.DIST.RANGE関数徹底解説：指定範囲の確率をまとめて計算！ 関連関数もご紹介

このブログでは、ExcelのBINOM.DIST.RANGE関数について詳しく解説し、さらに二項分布に関連する他の関数もご紹介します。BINOM.DIST.RANGE関数は、二項分布において、特定の範囲の成功回数が発生する確率を効率的に計算するのに役立ちます。

二項分布とは？

二項分布は、成功確率が一定の独立な試行を複数回行った場合に、成功する回数の確率分布を表します。例えば、コイン投げ、サイコロの特定の目が出る回数、製品検査での不良品数などが二項分布に従います。

BINOM.DIST.RANGE関数とは？

BINOM.DIST.RANGE関数は、指定された試行回数と成功確率において、指定された成功回数の範囲における確率の合計を計算します。つまり、「X回以上Y回以下の成功回数が発生する確率」を一度に計算できる便利な関数です。

BINOM.DIST.RANGE関数の構文

Excel

BINOM.DIST.RANGE(試行回数, 成功確率, 成功数1, [成功数2])

各引数の意味は以下のとおりです。

• 試行回数（必須）: 独立した試行の回数を指定します。正の整数である必要があります。
• 成功確率（必須）: 各試行が成功する確率を指定します。0以上1以下の数値である必要があります。
• 成功数1（必須）: 確率を計算する成功回数の下限を指定します。0以上の整数で、成功数2以下である必要があります。
• 成功数2（省略可能）: 確率を計算する成功回数の上限を指定します。省略すると、成功数1で指定された回数ちょうど成功する確率が計算されます。

BINOM.DIST.RANGE関数の使用例（画像に基づく例）

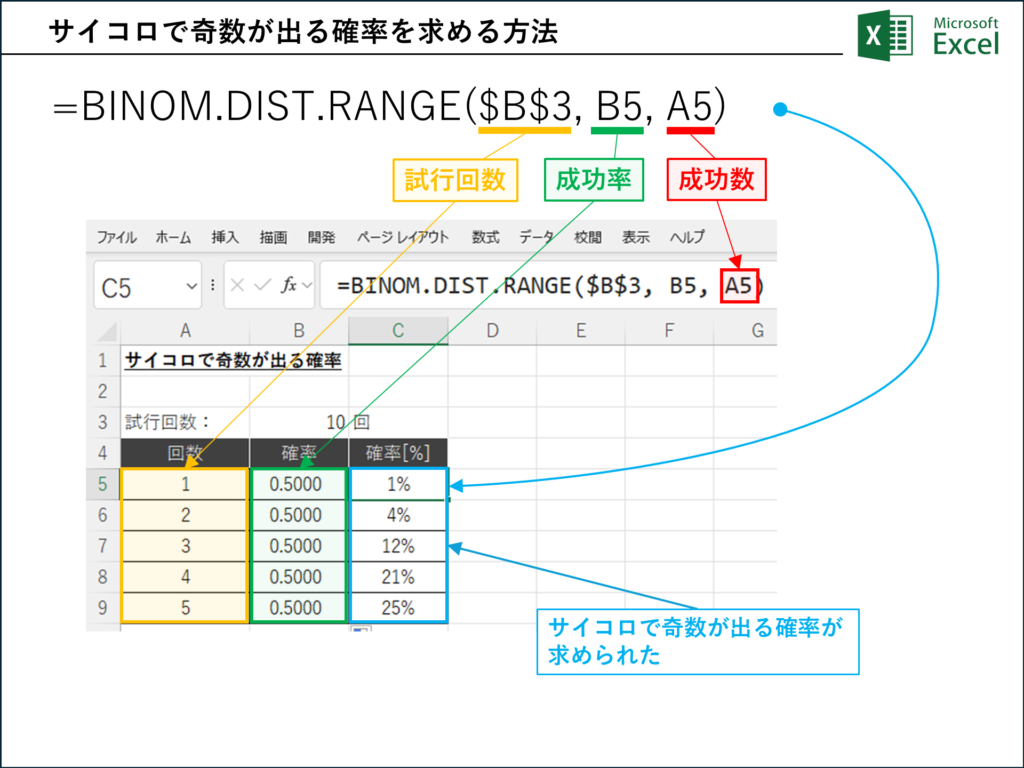
上記画像では、以下の設定でBINOM.DIST.RANGE関数を使用しています。

• 試行回数: 10回 (セルB3に格納)
• 成功確率: 0.5 (50%) (サイコロで奇数が出る確率)

画像に示されている数式は以下のとおりです。

Excel

=BINOM.DIST.RANGE($B$3, 0.5, A5)

この数式は、成功数2を省略しているため、「A5セルに格納された回数ちょうど成功する確率」を計算します。

画像では、A5からA9に1から5までの数字が入力されているため、それぞれ1回成功する確率、2回成功する確率…5回成功する確率が計算されています。

具体的な計算と画像の解釈：

画像では、B列に計算結果（確率）、C列にその確率をパーセント表示したものが示されています。

例えば、A5セルが1の場合、=BINOM.DIST.RANGE($B$3, 0.5, 1) は、「10回の試行で、成功確率が0.5の場合に、ちょうど1回成功する確率」を計算します。結果は約0.00977 (約1%) となります。

同様に、A6セルが2の場合、=BINOM.DIST.RANGE($B$3, 0.5, 2) は、「10回の試行で、成功確率が0.5の場合に、ちょうど2回成功する確率」を計算します。結果は約0.04395 (約4%) となります。

以下、同様に計算されます。

成功数2を指定する場合：

例えば、「3回以上5回以下成功する確率」を計算したい場合は、以下のような数式を使用します。

Excel

=BINOM.DIST.RANGE($B$3, 0.5, 3, 5)

この場合、3回成功する確率、4回成功する確率、5回成功する確率の合計が計算されます。

Excelサンプルデータのダウンロード

上記画像のエクセルサンプルデータを、以下のリンクからダウンロードできますので、練習用として活用ください。

【Excel】練習用サンプルデータ（例題）をダウンロード（無料）

BINOM.DISTとの違い（再掲）

BINOM.DIST関数で同じことを行うには、各成功回数に対してBINOM.DIST関数を個別に計算し、その結果を合計する必要があります。BINOM.DIST.RANGE関数を使えば、範囲指定で一度に計算できるため、より効率的です。

例：「3回以上5回以下成功する確率」をBINOM.DISTで計算する場合：

Excel

=BINOM.DIST(3, $B$3, 0.5, FALSE) + BINOM.DIST(4, $B$3, 0.5, FALSE) + BINOM.DIST(5, $B$3, 0.5, FALSE)

まとめ

BINOM.DIST.RANGE関数は、二項分布において特定の範囲の成功回数が発生する確率を効率的に計算できる便利な関数です。特に、範囲を指定して確率を求めたい場合に非常に役立ちます。

関連関数

BINOM.DIST

BINOM.DIST関数は、特定の回数ちょうど成功する確率、またはそれ以下の回数成功する累積確率を計算します。

• BINOM.DIST(成功数, 試行回数, 成功確率, FALSE): ちょうど指定された回数成功する確率（確率質量関数）
• BINOM.DIST(成功数, 試行回数, 成功確率, TRUE): 指定された回数以下成功する累積確率（累積分布関数）

CRITBINOM

CRITBINOM関数は、累積二項分布が基準値以上になる最小の成功回数を返します。例えば、「90%以上の確率で成功するには、最低何回試行する必要があるか」などを計算する際に使用します。

構文：CRITBINOM(試行回数, 成功確率, 基準確率)

N.DIST

N.DIST関数は、正規分布の確率密度関数または累積分布関数を計算します。試行回数が非常に大きい場合、二項分布は正規分布で近似できるため、N.DIST関数が役立つ場合があります。

構文：N.DIST(x, 平均, 標準偏差, 累積)

注意点（再掲）

• 引数に数値以外の値を指定すると、エラー値#VALUE!が返されます。
• 試行回数が0未満の場合、エラー値#NUM!が返されます。
• 成功確率が0未満または1より大きい場合、エラー値#NUM!が返されます。
• 成功数1が成功数2より大きい場合、エラー値#NUM!が返されます。

このブログで紹介した関連関数も合わせて活用することで、二項分布の分析がより深く行えるはずです。